Week 2 Day 1: Fast Modular Exponentiation - The Secret Weapon
Welcome to Week 2! Now that we have the number theory basics, we move to Modular Arithmetic.
The first stop is a technique so essential that many standard libraries implement it by default (but sadly, JavaScript’s Math.pow doesn’t support modular arithmetic directly).
The Problem
Calculate $(a^b) \pmod m$.
Example: Calculate $(3^{1000000007}) \pmod 7$.
If you try Math.pow(3, 1000000007) % 7, you’ll get Infinity or NaN because the number is too big to fit in a standard integer (or even a double).
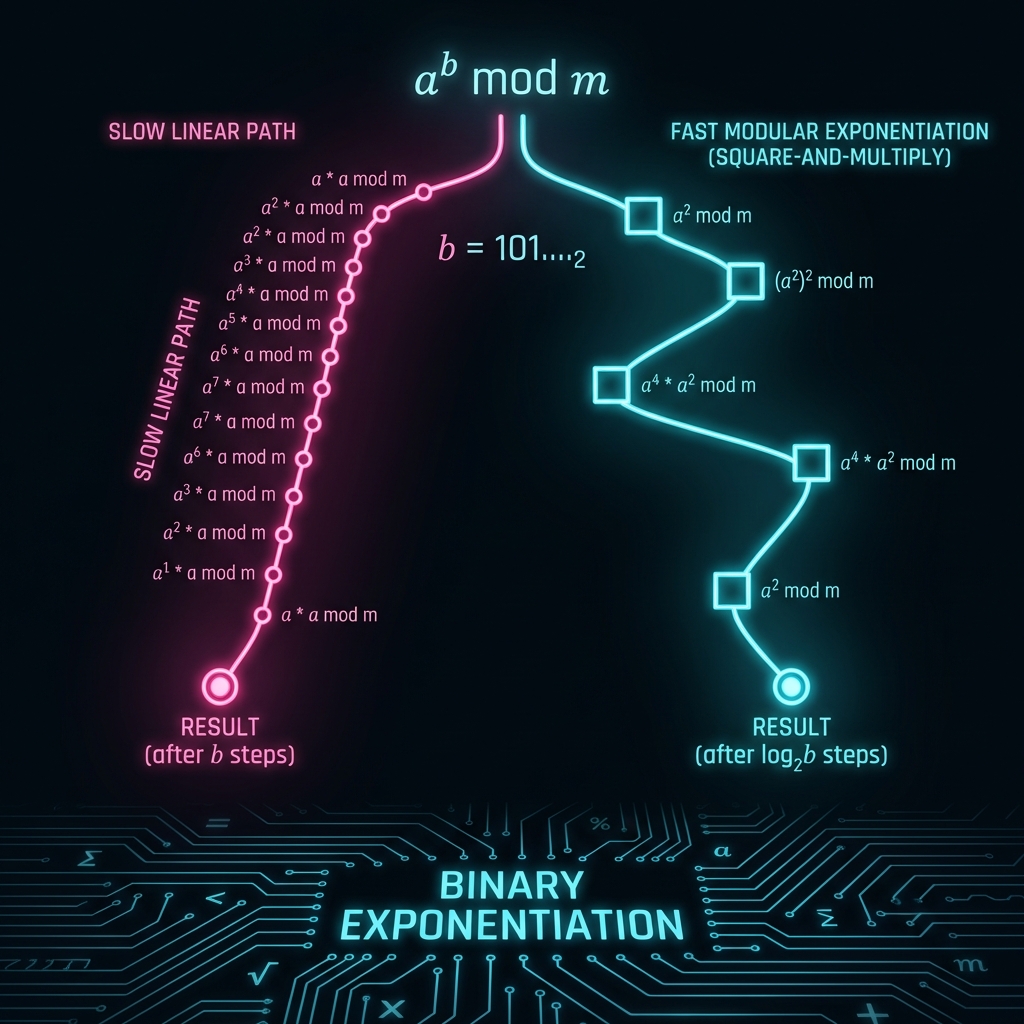
The Naive Solution (Too Slow)
function slowPower(base, exp, mod) {
let res = 1;
for (let i = 0; i < exp; i++) {
res = (res * base) % mod;
}
return res;
}
Time Complexity: $O(b)$. If $b = 10^9$, this takes seconds. If $b = 10^{18}$, it takes centuries.
The Fast Solution: Binary Exponentiation
We can compute $a^b$ in $O(\log b)$ time using the “Square and Multiply” method.
Logic: $$ a^{10} = a^5 \times a^5 = (a^2 \times a^2 \times a)^2 $$ We reduce the exponent by half at each step!
- If $b$ is even: $a^b = (a^{b/2})^2$
- If $b$ is odd: $a^b = a \times (a^{b-1})$
Implementation (JavaScript)
We need BigInt for safety with large numbers in JS.
/**
* Computes (base^exp) % mod efficiently.
* Time Complexity: O(log exp)
*/
function fastPow(base, exp, mod) {
let res = 1n;
base = BigInt(base) % BigInt(mod);
exp = BigInt(exp);
const modBI = BigInt(mod);
while (exp > 0n) {
// If exp is odd, multiply base with result
if (exp % 2n === 1n) {
res = (res * base) % modBI;
}
// Square the base
base = (base * base) % modBI;
// Divide exp by 2
exp /= 2n;
}
return Number(res);
}
console.log(fastPow(3, 13, 7)); // Output: 3
// 3^13 = 1594323
// 1594323 % 7 = 3
Why does this work?
Every number can be written in binary. $13 = 1101_2 = 8 + 4 + 1$. So $3^{13} = 3^8 \times 3^4 \times 3^1$. Our loop iterates through the bits of the exponent. If the bit is 1, we multiply the current power of $a$.
Challenge
Implement this recursively.
Compare the execution time of slowPower vs fastPow for $b = 10^9$.
See you on Day 2, where we tackle the tricky rules of Medieval Arithmetic (Modular Addition, Subtraction, Multiplication, and Division)! 🧙♂️