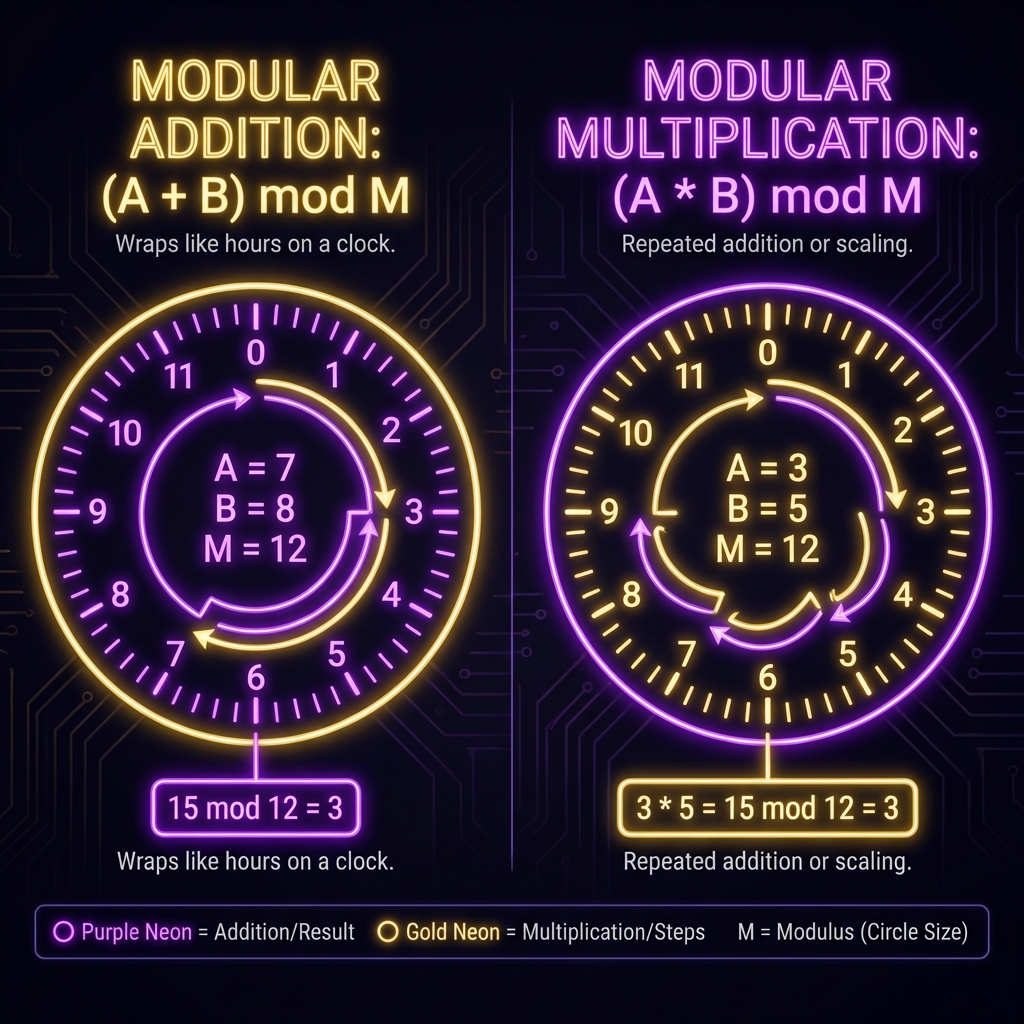
Week 2 Day 2: The Rules of Modular Arithmetic
Today we formalized the rules of the “Clock World”.
In modular arithmetic, we deal with integers in the range $[0, m-1]$. When we go past $m-1$, we wrap around to 0.
1. The Safe Operations
Addition, Subtraction, and Multiplication behave nicely. You can apply the modulo operator at each step to keep numbers small.
Properties
- Addition: $$(A + B) \pmod m = ((A \pmod m) + (B \pmod m)) \pmod m$$
- Multiplication: $$(A \times B) \pmod m = ((A \pmod m) \times (B \pmod m)) \pmod m$$
- Subtraction: $$(A - B) \pmod m = ((A \pmod m) - (B \pmod m) + m) \pmod m$$ Note: We add $m$ to handle negative results!
Why is this essential?
In coding problems, you are often asked to output the answer modulo $10^9 + 7$. If you calculate $A \times B \times C$ directly, it might overflow 64-bit integers. Instead, you do:
let ans = 1;
ans = (ans * A) % mod;
ans = (ans * B) % mod;
ans = (ans * C) % mod;
2. The Dangerous Operation: Division
Here is the trap: $$ (A / B) \pmod m \neq ((A \pmod m) / (B \pmod m)) \pmod m $$
Example: $$ (10 / 2) \pmod 3 = 5 \pmod 3 = 2 $$ $$ ((10 \pmod 3) / (2 \pmod 3)) = (1 / 2) \dots \text{Undefined in integers!} $$
So how do we divide?
We don’t. We multiply by the inverse. $$ (A / B) \pmod m \equiv (A \times B^{-1}) \pmod m $$
But what is $B^{-1}$? It’s the Modular Multiplicative Inverse. This only exists if $B$ and $m$ are coprime ($\text{GCD}(B, m) = 1$).
We will learn how to find this magical number tomorrow!
3. Practice Problem
Given an array of numbers, find the product of all elements modulo $10^9 + 7$.
function arrayProduct(arr) {
const MOD = 1000000007n;
let product = 1n;
for (let num of arr) {
product = (product * BigInt(num)) % MOD;
}
return Number(product);
}
See you on Day 3 for the Modular Inverse! 🔄