Week 1 Day 4: Finding Primes Fast - The Sieve of Eratosthenes
Welcome to Day 4! Today we tackle a problem that has fascinated mathematicians for millennia: Prime Numbers.
Specifically, how do we find all prime numbers up to a limit $N$?
1. The Naive Approach
A common mistake is to loop from 1 to $N$ and for each number, check if it’s prime.
// Slow: O(N * sqrt(N))
function getPrimes(N) {
const primes = [];
for (let i = 2; i <= N; i++) {
if (isPrime(i)) primes.push(i);
}
return primes;
}
If $N = 10^7$, this will take forever. We can do better.
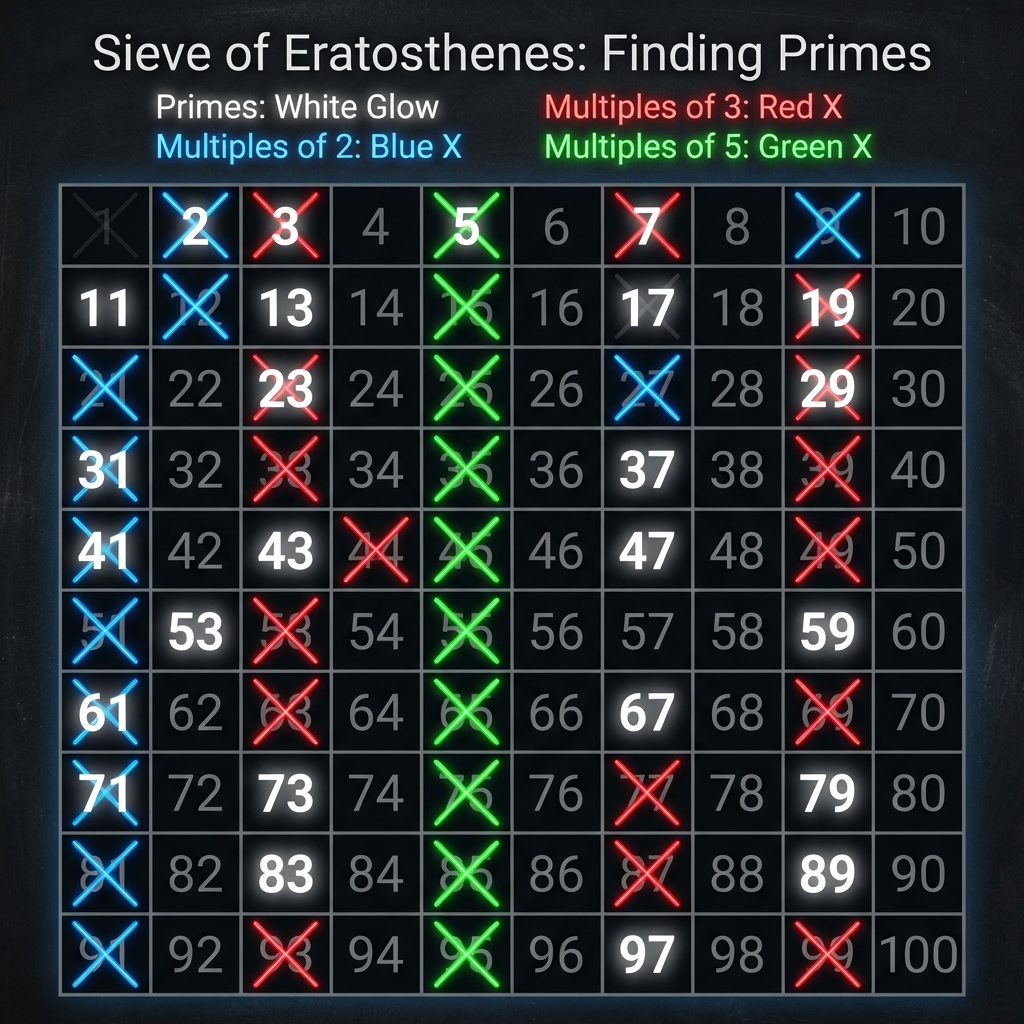
2. The Sieve of Eratosthenes
The algorithm works by elimination.
- Write down all numbers from 2 to $N$.
- Start with the first number (2). It’s prime.
- Cross out all multiples of 2.
- Move to the next non-crossed number (3). It’s prime.
- Cross out all multiples of 3.
- Continue until you reach $\sqrt{N}$.
Visual Logic
It’s like filtering sand through a sieve—only the prime numbers stay.
3. Implementation
/**
* Generates all primes up to N using the Sieve of Eratosthenes.
* Time Complexity: O(N log log N)
* Space Complexity: O(N)
*/
function sieve(n) {
const isPrime = new Array(n + 1).fill(true);
isPrime[0] = isPrime[1] = false;
// We only need to sieve up to sqrt(n)
for (let i = 2; i * i <= n; i++) {
if (isPrime[i]) {
// Mark multiples starting from i*i
for (let j = i * i; j <= n; j += i) {
isPrime[j] = false;
}
}
}
const primes = [];
for (let i = 2; i <= n; i++) {
if (isPrime[i]) primes.push(i);
}
return primes;
}
const primes = sieve(50);
console.log(primes); // [2, 3, 5, 7, 11, 13, 17, 19, 23, 29, 31, 37, 41, 43, 47]
Why j = i * i?
Notice the optimization: let j = i * i.
When sifting multiples of 5, we start at 25 ($5 \times 5$). Why?
Because $5 \times 2$ was crossed out by 2.
$5 \times 3$ was crossed out by 3.
So we skip redundant work!
4. Time Complexity
The complexity is $O(N \log \log N)$, which is almost linear. For $N = 10^7$, it runs in a fraction of a second.
5. Coding Challenge
What if $N$ is huge (up to $10^{14}$) but the range $[L, R]$ is small ($R - L < 10^6$)? You can’t create an array of size $10^{14}$. This requires the Segmented Sieve, a technique we’ll explore in advanced topics.
Tomorrow, we wrap up Week 1 by learning how to break composite numbers back down into primes using Prime Factorization.
See you on Day 5!