Week 1 Day 2: The Euclidean Algorithm - Speeding up GCD
Welcome back! Yesterday we learned what GCD is. Today, we learn the best way to find it.
The Euclidean Algorithm is named after the ancient Greek mathematician Euclid, who described it in his “Elements” (c. 300 BC). It is a recursive method for finding the GCD of two numbers that is exponentially faster than the brute-force method.
1. The Core Idea
The algorithm relies on a simple yet powerful principle:
If $A > B$, then $\text{GCD}(A, B) = \text{GCD}(A - B, B)$
Eventually, if we keep subtracting the smaller number from the larger one, we end up with 0. The non-zero number at that step is our GCD.
However, repeated subtraction is slow. We can speed it up using the modulo operator (remainder).
$\text{GCD}(A, B) = \text{GCD}(B, A \pmod B)$
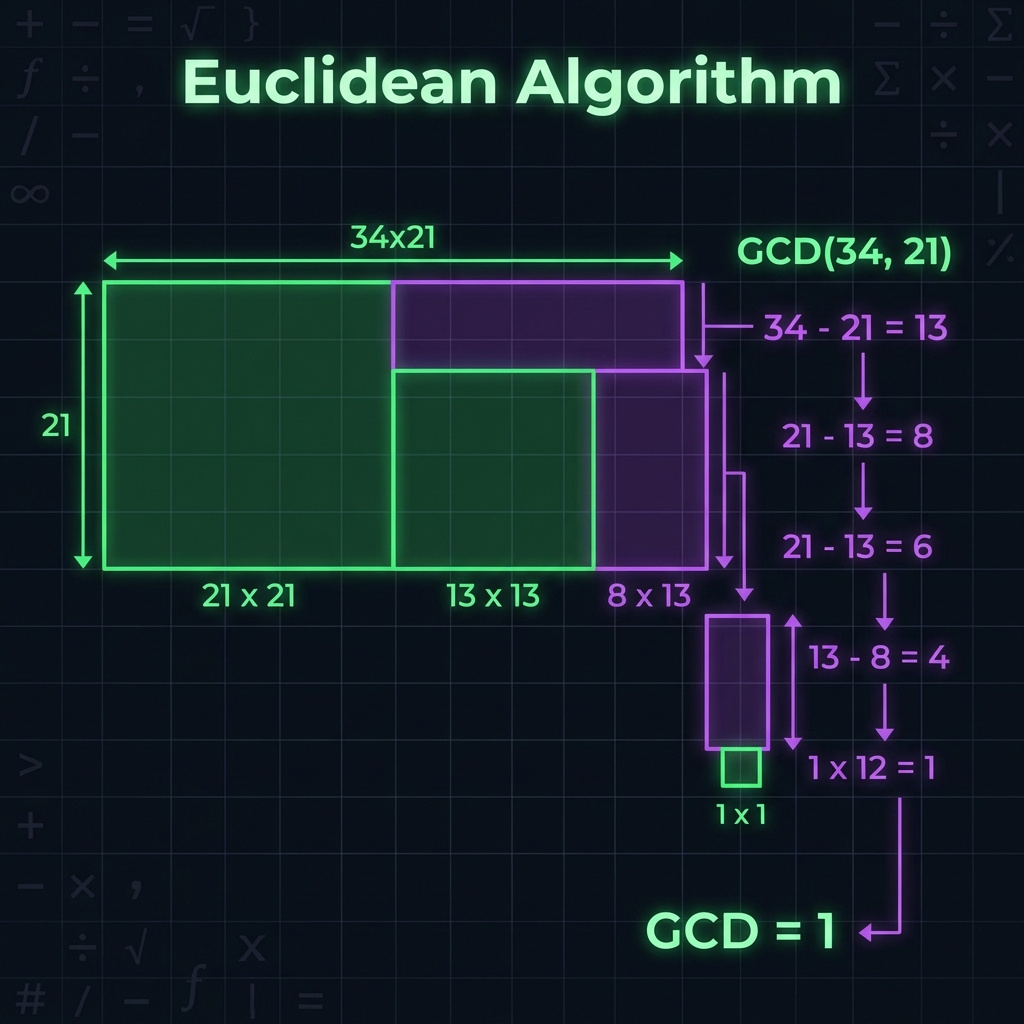
2. Geometric Interpretation
Imagine a rectangle with dimensions $A \times B$. Finding the GCD is equivalent to tiling this rectangle with the largest possible square involved.
- We fill the rectangle with $B \times B$ squares.
- We are left with a smaller rectangle of size $B \times (A \pmod B)$.
- We repeat the process for this smaller rectangle.
- When the remainder is 0, the side length of the square we used is the GCD.
3. Implementation Variants
Recursive (Elegant)
function gcd(a, b) {
if (b === 0) return a;
return gcd(b, a % b);
}
Iterative (Stack-Safe)
function gcdIterative(a, b) {
while (b !== 0) {
let temp = b;
b = a % b;
a = temp;
}
return a;
}
4. Time Complexity
Why is this “fast”?
In every step of the algorithm: a % b < a / 2.
This means the numbers shrink by at least half every two steps.
This gives us a time complexity of $O(\log(\min(A, B)))$.
For example, finding the GCD of two 100-digit numbers takes only a few hundred operations, whereas brute force would take forever!
5. Coding Challenge
Refactor yesterday’s LCM code to precise C++ or a strongly typed language (like TypeScript) and handle edge cases where inputs might be 0.
Hint: LCM(0, 5) is 0.
See you on Day 3, where we will apply LCM to solve real-world scheduling problems! 🗓️